Collaborative filtering

Collaborative filtering algorithms recommend items (this is the filtering part) based on preference information from many users (this is the collaborative part). The collaborative filtering approach is based on similarity; the basic idea is people who liked similar items in the past will like similar items in the future. In the example below, Ted likes movies A, B, and C. Carol likes movies B and C. Bob likes movie B. To recommend a movie to Bob, we calculate that users who liked B also liked C, so C is a possible recommendation for Bob. Of course, this is a tiny example. In real situations, we would have much more data to work with. The main task is to predict the ratings of the empty blocks for Carol and Bob.

Alternating Least Squares (ALS)

Spark MLlib implements a collaborative filtering algorithm called Alternating Least Squares (ALS). ALS approximates the sparse user item rating matrix of dimension K as the product of two dense matrices User and Item factor matrices of size U×K and I×K (see picture below).

The factor matrices are also called latent feature models. The factor matrices represent hidden features which the algorithm tries to discover. One matrix tries to describe the latent or hidden features of each user, and one tries to describe latent properties of each movie

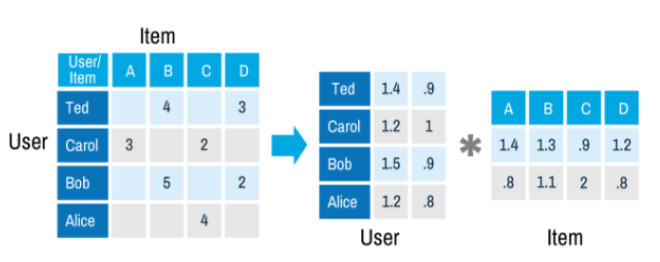
ALS is an iterative algorithm. In each iteration, the algorithm alternatively fixes one factor matrix and solves for the other, and this process continues until it converges. This alternation between which matrix to optimize is where the "alternating" in the name comes from.

lternating Least Squares (ALS) matrix factorization

ALS attempts to estimate the ratings matrix R as the product of two lower-rank matrices, X and Y, i.e. X * Yt = R. Typically these approximations are called 'factor' matrices. The general approach is iterative. During each iteration, one of the factor matrices is held constant, while the other is solved for using least squares. The newly-solved factor matrix is then held constant while solving for the other factor matrix.

This is a blocked implementation of the ALS factorization algorithm that groups the two sets of factors (referred to as "users" and "products") into blocks and reduces communication by only sending one copy of each user vector to each product block on each iteration, and only for the product blocks that need that user's feature vector. This is achieved by pre-computing some information about the ratings matrix to determine the "out-links" of each user (which blocks of products it will contribute to) and "in-link" information for each product (which of the feature vectors it receives from each user block it will depend on). This allows us to send only an array of feature vectors between each user block and product block, and have the product block find the users' ratings and update the products based on these messages.